DISEÑO DE ELEMENTOS DE TORSIÓN
Introducción
Un momento que actúa alrededor del eje
longitudinal de un elemento estructural se denomina “ momento torsor “ o “
torque “ y se denota con la sigla “ T “. En las estructuras la torsión se
origina por: a) la acción de cargas excéntricas en vigas, b) las deformaciones
producidas por la continuidad del sistema y c) el efecto producido por la
conexión lateral de elementos metálicos a vigas o columnas, figura 8.1.
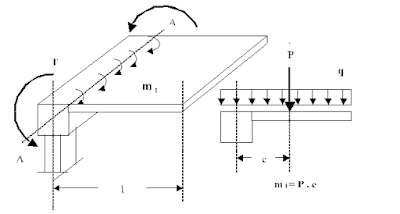
Figura 8.1 Representación de la torsión de equilibrio
Con frecuencia los elementos estructurales
están sometidos a la combinación de flexión ( M ), cortante ( V ) y carga axial
( N ); sin embargo la presencia de fuerzas que producen torsión ( T ) no
son excepcionales y a pesar de no ser tan frecuentes como las anteriores
producen un alabeo típico en los elementos cuando actúa en combinación con las
otras tres tensiones.
Por muchos años la torsión fue considerada como
un efecto estructural secundario y por lo tanto no fue incluida directamente en
los diseños por lo que el problema se resolvía considerando un factor total de
seguridad que conservadoramente se incluía en los cálculos. Sin embargo en las
ultimas cuatro décadas del siglo XX los efectos de daños en estructuras
afectadas por sismos mostraron evidencia de que el enfoque utilizado era
incorrecto, además los procedimientos de diseño se mejoraron aumentando la
esbeltez de las secciones y disminuyendo los factores de seguridad y finalmente
la ingeniería practica incremento el uso de estructuras donde la torsión era
una tensión importante como en el caso de puentes curvos, secciones en cajón y
escaleras en espiral. Lo anterior contribuyo a solicitar mayor investigación en
este campo.
Al estudiar la torsión es importante reconocer que existe: “ torsión estática
o primaria” y “ torsión hiperestatica o secundaria”. La primera es denominada
como “ torsión de equilibrio” y se presenta cuando las cargas externas que
producen torsión solo se pueden equilibrar con la capacidad resistente del
material. En estos casos la torsión requerida para mantener el equilibrio es
estáticamente determinada. Un ejemplo de este caso es la losa en voladizo de la
figura 8.1 en donde las cargas externas producen momentos torsores “ mt
“ que actúan longitudinalmente en la viga de apoyo “ A-A” y que son
equilibrados por el torsor resistente “ T “ suministrado por las columnas. Sin
la presencia de “ T “ la estructura colapsa. En contraste a esta condición se
presenta la “ torsión secundaria “ la cual proviene de la continuidad y compatibilidad
de deformaciones en el interior de los sistemas estructurales. En este caso los
momentos torsores no se pueden hallar solo por equilibrio estático, se debe
utilizar una redistribución interna de tensiones para luego aplicar el
equilibrio estático alternativo. Si se desprecia la continuidad en el diseño se
produce una gran fisuración de la estructura pero por lo general no colapsa. La
figura 8.2 ilustra la viga de borde de una losa de piso de una edificación
sometida a torsión secundaria.
Figura 8.2 Representación de la torsión secundaria
Si la viga de borde “ A-A “ es suficientemente
rígida a torsión y adecuadamente reforzada y si las columnas pueden soportar el
torque “T “ los momentos en la losa se aproximaran a los de un soporte rígido
como se muestra en el primer diagrama de momentos de la figura 8.1. Sin embargo
si la viga tiene poca rigidez torsional y un refuerzo inadecuado a torsión se
presenta su fisuración con la posterior caída de la rigidez y los momentos en la
losa se aproximan a los de un extremo articulado como se indica en el segundo
diagrama de momentos de las figura 8.2. Si la losa se diseña de acuerdo al
diagrama de momentos con viga de borde articulada, que es realmente como la
estructura trabaja, no se presenta el colapso.
Mientras las técnicas modernas para el análisis
estructural permiten una evaluación mas realista del momento torsor ( análisis
espacial ) tanto para condiciones estáticamente determinadas como
indeterminadas, por lo general en los diseños se desprecian los efectos de la
torsión secundaria cuando las tensiones a torsión son bajas y es posible usar
el equilibrio estático alternativo. Esto se permite en muchos códigos y
especificaciones de diseño. De otra parte cuando la resistencia a torsión es
importante, como en el caso de puentes, se requiere utilizar un análisis
riguroso del problema incluyendo un detallado completo de refuerzo a torsión
como se indicará mas adelante.
La primera recopilación organizada de
conocimientos y trabajos sobre la torsión fue realizada por el ACI y difundida
en un simposio en el año 1968 con el nombre de “ La torsión en el hormigón
estructural “. Las memorias del evento se publicaron con el mismo titulo y se
conocen como “ publicación especial SP # 18 del ACI ”. La mayor parte de las
referencias, tomadas en los códigos para estudiar la torsión, provienen de la
teoría clásica de la resistencia los materiales. La primera vez que el código
ACI incorpora recomendaciones detalladas para el diseño a torsión es en la
versión 318-71 en donde se basa en toda la información experimental obtenida
hasta la fecha.
8.2 La torsión en la resistencia de materiales
8.2.1 Secciones sólidas
Figura 8.3 Torsión en secciones sólidas
En un elemento sometido a torsión, el momento
torsor “ mt “ produce tensiones cortantes “ ô “ en su sección
transversal tanto radial como
tangencialmente. La figura 8.3 ilustra este efecto en una barra empotrada sometida
en un extremo a un momento torsor “ T “. El resultado es un campo de tensiones
cortantes que actúan en forma similar a la indicada en el elemento diferencial
“ 1 “.
En un elemento de sección circular sólida las
tensiones cortantes son nulas en el eje y máximas en su perímetro aumentando
linealmente como se aprecia en la figura 8.3. En forma similar la sección
cuadrada presenta una configuración similar de tensiones cortantes con el
agravante de que las tensiones en el perímetro varían de cero en las esquinas a
un máximo en el centro del borde.
La representación mas clásica de las tensiones
cortantes generadas por la torsión la suministra la teoría de la elasticidad
usando la analogía de la película de jabón. Las ecuaciones para expresar la pendiente
de una lamina en forma de cúpula son análogas a las ecuaciones para las
tensiones cortantes producidas por la torsión.
Se concluye por tanto que si se toma una lamina
o placa y se hace en su centro una abertura de forma similar a la sección analizada
y se cubre luego la abertura con una película de jabón, al inflarse la película
se forma una superficie curva que representa el campo de tensiones a torsión.
La pendiente máxima en cada punto de la curva es proporcional a las tensiones
cortantes en el punto.
Figura 8.4 Analogía de la película de jabón en diseño a
torsión
Para obtener la expresión general de la torsión en secciones sólidas,
homogéneas, elásticas e isotrópicas se asumirá un elemento diferencial en forma
de disco de espesor “ dx “ y radio “ r “ sometido a un torque “ T “ , figura
8.5. Aislando el disco diferencial de la sección se tiene que al aplicar un
torsor diferencial “ dT “ la cuerda “ a-b ” se desplaza a “ a´- b´ “ realizando
un giro “ dÖ “
Figura 8.5 Elemento diferencial de disco a torsión
Para ángulos pequeños se puede considerar: dÖ =
ds / r. Considerando la sección abcd:
Se llega a la conclusión de que “ ã = r è “. En el rango elástico se asume
que las tensiones cortantes son proporcionales a las deformaciones por cortante
=> ô ã £ ô = G. ã Donde G : modulo de cortante
Las tensiones cortantes de un elemento
superficial son: ô = G.r. è y para un elemento interior son : ô = G.ñ. è
Si se incluye ahora el torque externo “ T “ se
tiene:
T =∫t .dA.r = ∫G.r .q.r .dA
T = G.q.∫r 2dA
∴T = G.q.J
J : Momento polar de inercia
Jcirc = p.2r4
Esta es la expresión reconocida de la
resistencia de materiales y determina la tensión cortante en función del
momento torsor y las propiedades geométricas de la sección. Si se mantiene
recto el eje del cilindro y se aumenta gradualmente la deformación en la
sección se aprecia que la región interna cercana al eje permanece en rango
elástico mientras que la zona de los bordes comienza a plastificarse como se muestra en la figura 8.6. Cuando la
sección se plastifica totalmente las tensiones cortantes no son proporcionales
al momento torsor aplicado y se produce la falla para un cortante de =>
Figura 8.6 Distribución de tensiones cortantes por
torsión en una sección circular
En una sección rectangular maciza el problema
de la torsión es mas complejo. Las secciones inicialmente planas sufren alabeo
bajo la acción de los momentos torsores. Este momento produce tensiones
cortantes axiales y circunferenciales con valores de cero en las esquinas y el
centro del rectángulo y máximas en los puntos medios de los bordes laterales
como se indica en la figura 8.3. Este campo de tensiones hace difícil presentar
una formulación racional similar a las ecuaciones para la sección circular. Afortunadamente
la teoría de elasticidad permite desarrollar la expresión 8.3 para representar
el estado de tensiones cortantes en secciones rectangulares cuya deducción esta
fuera del alcance de este texto.
t max
= T2.y a .x
En donde T: torque aplicado en la sección, x:
lado corto, y : lado largo y á: coeficiente numérico que depende de la relación
( y / x ). En general se puede utilizar
la ecuación 8.4 para hallar en forma aproximada el valor de á.
Secciones huecas o en cajón
Si en una estructura la torsión es la tensión
predominante la sección tubular es la optima para resistir el campo de
tensiones originado. En el numeral anterior se indico que las tensiones
cortantes originadas por la torsión son mayores en los bordes y prácticamente
nulas en el eje. Esto lleva a la
conclusión de que en estos casos el núcleo de las secciones es inútil para
resistir torsión y lo mas lógico es que esta parte no se requiere para resistir
tensiones originando la forma hueca o cajón. La figura 8.7 representa un
cilindro hueco o tubo de un material ideal, elástico, homogéneo e isotropico,
el cual esta empotrado en un extremo y sometido a un torque “ mt “
en el otro.
Figura 8.7 Torsión en secciones huecas
El momento torsor aplicado es: mt =
P.a
El ángulo de giro de la sección es “ Ö “ £ ( Ö / L )
= Cte. = è
Si se define como “ Ao “ el área del
radio medio de la sección =>
T = 2.Ao.t .t = 2.Ao.q
Comparando las ecuaciones 8.1 y 8.5 se nota
como para un mismo torsor las tensiones cortantes en la sección hueca son
mayores que las de la sección maciza. Si por ejemplo se tiene un cilindro
sólido de acero con 50 mm de diámetro sometido a un torsor de 4.0 kN.m => ô
= 163 MPa. Si el cilindro es hueco del mismo diámetro y con espesor
t = 5 mm se tiene para el mismo torsor aplicado: ô = 251 MPa es decir un
54% mayor que las tensiones de la sección sólida. Esto lleva a la conclusión de
que es mas confiable y seguro trabajar con la sección hueca para el diseño
estructural a torsión. En definitiva se puede asumir que las tensiones
cortantes “ ô “ son constantes a través de un espesor “ t “ en la periferia de
la sección por tanto la sección es similar a un tubo de pared delgada en donde
la torsión es resistida por unas fuerzas perimetrales de corte denominadas “
flujo de corte: q “.
En el caso de una sección rectangular la
expresión 8.5 tiene la misma deducción. La figura 8.8 muestra una sección cajón
de dimensiones medias “ X , Y “ sometida a un
momento torsor “ T “.
Figura 8.5 Sección hueca rectangular sometida a torsión
Si se toman momentos alrededor del eje central
de la sección se tiene:
Teoría de la Torsión en el hormigón
sin refuerzo
Utilizando los conceptos estudiados en el
numeral anterior el problema de la torsión en el hormigón se puede enfocar de
dos formas: 1) cuando este no lleva ningún refuerzo metálico ( sección solo de
hormigón ) y 2) cuando lleva refuerzo longitudinal y transversal en su sección
( hormigón armado).
En el primer caso se pueden considerar así
mismo dos procedimientos: el utilizado por la teoría clásica de elasticidad
llamado “ la torsión de Saint Venant “ y el utilizado por la teoría de
plasticidad o la torsión en tubos de pared delgada. En la elasticidad se indica
que las tensiones producidas por la torsión se distribuyen en la forma indicada
en la figura 8.3 y se calculan usando la expresión 8.3. Estas tensiones se
deben convertir luego en tensiones principales para hallar aquellos puntos de
máxima tracción y compresión y así finalmente definir las líneas de fractura
del material. El desarrollo completo de esta teoría marcó la forma de proceder
en la ingeniería Americana hasta mediados de la década del 90. Se le conoce mas
técnicamente como la “ teoría de la flexión oblicua o teoría de Hsu “. Por el
contrario en la teoría de la sección hueca se utiliza la analogía de la cercha
espacial para obtener el campo de tensiones en la sección llegando a la
expresión 8.5. Esta forma de proceder se
popularizo primero en Europa y Canadá para finalmente hacerlo a finales de la
década del 90 en Estados Unidos. Se le conoce como la teoría de la “ cercha
espacial o analogía de la cercha”.
8.3.1
Teoría de la flexión oblicua “ Hsu “
Cuando se somete un elemento de hormigón a torsión pura ( caso ideal )
las fisuras se presentan cuando las máximas tensiones principales a
tracción “ ó t “ alcanzan el
valor de la resistencia a la tracción del hormigón “ f´t “.
Ya que las tensiones principales a tracción
dependen o son proporcionales a las tensiones cortantes en cualquier punto del
elemento, el torque “ T “ en el momento de la fisuración puede obtenerse
igualando la expresión 8.3 a “ f´t “.
Donde: Tcr
= Momento torsor de fisuración del hormigón. Si el comportamiento es elástico
=> se puede asumir con base en resultados experimentales que á = ( 1 / 3 ) y
que “ f´t = 0.80 [ 0.63 ( f´c )0.5 ]= 0.5 (
f´c)0.5 “. El momento torsor de fisuración se puede expresar para
secciones rectangulares.
Un aspecto importante de esta teoría es conocer
porque la torsión se traduce en una flexión oblicua. Para ello es necesario
estudiar como es la superficie de falla producida por este estado de tensiones. La figura 8.7
muestra como la fisura a torsión es una espiral que envuelve la sección y
cuando completa un ciclo de 360° genera una superficie de falla inclinada cuyo
ángulo se puede considerar para propósitos de análisis como de 45°. Esta
superficie inclinada es mas una falla por flexión que por cortante.
Figura 8.7 Flexión oblicua por torsión
Utilizando la geometría de la sección “ 1234 “
se tiene:
T T
Torsión pura en el hormigón armado
Numerosos ensayos indican que la presencia de solo barras longitudinales en una sección de hormigón incrementan su resistencia a torsión en aproximadamente un 15% debido a la acción de dovela que ejerce este acero, impidiendo la falla por hendimiento del material. En este sentido se puede decir que la capacidad a torsión del hormigón armado sin refuerzo transversal se puede considerar en forma conservadora como la expresada por las ecuaciones 8.8 y 8.9.
Figura 8.8 Torsión en el hormigón armado
En el caso general, cuando la sección tiene
acero longitudinal y transversal adecuadamente detallado, como se ilustra en la
figura 8.8, se puede decir que en el instante que T T cr el hormigón se fisura e inmediatamente su
resistencia a torsión disminuye en un 50% mientras que el acero de refuerzo
comienza a trabajar soportando la torsión excedente. Esta redistribución de
tensiones internas permite entender el porque se presenta una etapa de fluencia
en la curva torsión-giro ( T vs è ) del material. Cuando la sección alcanza su
máxima resistencia la capa de hormigón que recubre el refuerzo comienza a
desintegrarse desprendiéndose de la sección lo que finalmente se traduce en la
perdida de aporte de resistencia a torsión del hormigón.
Al igual que en el caso del hormigón sin
refuerzo existen dos teorías que permiten resolver el problema de la torsión en
el hormigón armado: La teoría de Hsu ( clásica ) y la teoría de la cercha
espacial ( moderna).
8.4.1
Teoría de Hsu o de la flexión oblicua
Este enfoque fue el propuesto por el ACI-318
desde el año 1971 hasta el año 1989 y se basa en los primeros resultados
experimentales de los ensayos realizados en los Estados Unidos para tratar de
proponer una metodología racional a la solución del problema de la torsión en
el hormigón armado. En este enfoque se parte de la hipótesis de que tanto el
hormigón como el refuerzo aportan resistencia a torsión en una sección,
considerando la torsión nominal como la suma de las dos contribuciones:
Tn = Tc + Ts
Tc : Resistencia a torsión
suministrada por el hormigón
Ts : Resistencia a torsión
suministrada por el refuerzo
Tn : Resistencia a torsión nominal
del hormigón armado
Figura 8.9 Sección de hormigón armado sometida a torsión
Utilizando el mismo enfoque de la sección de
hormigón sin refuerzo, cuando la sección se fisura se genera una superficie de
falla inclinada similar a la de la figura 8.7 pero ahora se incluye la
presencia del acero longitudinal y transversal.
En cada cara, la fisura es cruzada por un
determinado numero de estribos “ n “ mientras en la zona comprimida de la
sección se genera una resultante horizontal que debe ser equilibrada por
refuerzo longitudinal.
Experimentalmente se ha comprobado que en la
falla las ramas verticales de los estribos entran en fluencia mientras que las
ramas horizontales permanecen en rango elástico. En consecuencia el par que
produce giro debido a las fuerzas horizontales es:
Después de la fisuración el área encerrada por
el flujo de cortante es “ xo.yo “ medidos desde los
centroides del acero. Se define: Ao = xo.yo y Po = 2 ( xo + yo
). El modelo físico que se utiliza para el análisis es una armadura espacial en
donde unos elementos están en tracción y otros en compresión. Los primeros son
los estribos y barras longitudinales y los segundos el hormigón.
En la figura 8.11 se aprecia como cada cara
lateral aporta resistencia a torsión. La cara donde actúa “ V4 “ aporta una torsión:
T4 = V4.xo
2
Ahora V4 es la cortante que actúa en
la cara “ cc´bb´ “ es equilibrada
por la resultante a tracción de cada una de las ramas verticales de los
estribos que cortan las fisuras.
Aislando la cara “ cc´bb´ “, figura 8.12 y considerando que la rama vertical del
estribo entra en fluencia cuando se alcanza la resistencia a torsión se tiene:
∑Fy = 0 ⇒V4 −n.(At.fyv )= 0
En el equilibrio anterior no se considero el
aporte de los puntales de hormigón a compresion en cada cara. La figura 8.13
ilustra gráficamente como es el trabajo de estos bloques bajo la acción de un
torsor “ T “.
La fuerza cortante “ V4 “ se puede
descomponer en dos fuerzas, una en dirección de los puntales “ D4 “
y la otra longitudinal “ N4 “.
N4 = V4.Cot(q)
D4 = V4 Sen(q)
Sen(q)



















No hay comentarios:
Publicar un comentario