LOSAS ARMADAS EN DOS DIRECCIONES
10.1
Introducción
En las
edificaciones de hormigón armado las losas son aquellos elementos estructurales
planos que permiten en primer lugar suministrar superficies de apoyo a las
cargas verticales sean estas vivas o muertas y en segundo termino actuar como elemento de amarre ( diafragma )
al sistema de columnas y muros que es en definitiva el que soporta la
estructura, figura 10.1.
Figura 10.1 Representación esquemática de las losas de
edificios
La losa
puede apoyarse directamente sobre columnas o descansar sobre muros cargueros,
vigas de hormigón o de acero generando así diferentes de condiciones de apoyo
que indican formas especiales de trabajo estructural. Por ejemplo si la losa se
apoya en todo su perímetro sobre vigas cargueras rígidas o sobre muros se tiene
el sistema de “ Losas perimetralmente apoyadas ” el cual puede trabajar en una
o dos direcciones de acuerdo a la relación de sus lados, figura 10.2.b. Si la
losa se apoya en solo dos vigas o muros cargueros se tiene la “ losa en una
dirección ”, figura 10.2.a. Si finalmente se apoya directamente sobre las
columnas se generan dos tipos de superficies únicas en el hormigón armado: “ la
losa plana y la placa plana “, figura 10.3.
Igualmente una losa puede ser completamente
sólida o contener cavidades vacías, en el primer caso de tiene la “ Losa maciza
“ y en el segundo “ la losa aligerada “. La losa aligerada es la mas utilizada
en los edificios porque al permitir disminuir el peso propio
a) losa en una dirección b)
losa en dos direcciones apoyada sobre vigas o muros cargueros
Figura 10.2 Sistemas de losa en una y dos direcciones
Figura 10.3 Sistemas de placa plana y losa plana
de las
edificaciones se disminuye el costo. La losa maciza es utilizada en los
tableros de puentes por su alta capacidad estructural, figura 10.4.
Figura 10.4 Sección de losa maciza y aligerada de
hormigón armado
Adicionalmente a los tipos de losas indicados,
existen otras que se apoyan en toda su superficie como los pisos de edificios,
pavimentos de vías, pisos de bodegas y parqueaderos que requieren un
tratamiento diferente a las anteriormente mencionadas.
El refuerzo en las losas se coloca en forma
convencional en dirección paralela a las superficies planas superior e
inferior, sin embargo en el caso de losas de puentes, se pueden utilizar acero
doblado a 45° que permite resistir tensiones por flexión positivas y negativas
sin interrumpir longitudinalmente el refuerzo. Se puede utilizar también mallas
electrosoldadas como refuerzo en losas y acero de alta resistencia en forma de
cables para losas postensadas.
LOSAS ARMADAS EN DOS DIRECCIONES
Existen varios tipos de losas armadas en dos direcciones. Las más antiguas, estudiadas en códigos, por ejemplo del ACl-63, son las losas planas apoyadas en vigas. Este método todavía es aceptable actualmente, aunque el reglamento ACl11 no lo menciona en las normas peruanas.
En la actualidad se utilizan losas planas sin vigas, losas planas con capiteles o ábacos, losas con casetones. Todas ellas se usan de acuerdo al caso específico, ya sea por requerimientos de altura del piso, espesor de losa, necesidades de instalaciones, facilidades constructivas, limitaciones del esfuerzo-cortante, luces entre apoyos, magnitud de cargas vivas y/o cargas muertas, etc.
El Código ACI considera dos tipos de análisis para losas armadas en dos sentidos:
- El método directo de diseño y;
- El método del marco o pórtico equivalente
Además se considera el método de los coeficientes utilizados en el ACl-63, el mismo que nunca fue prohibido.
Los tres métodos indicados están concebidos con métodos aproximados al análisis.
El proyectista puede utilizar métodos más exactos de análisis en base a soluciones numéricas como líneas de influencia u otros métodos teóricos siempre y cuando cumpla con los criterios de seguridad y servicio solicitados por el ACI.
CRITERIOS PARA EL DIMENSIONAMIENTO DE
LOSAS ARMADAS EN DOS SENTIDOS
Franja de Diseño
Para analizar un sistema de losas en dos
direcciones ya sea mediante el Método de Diseño Directo o mediante el Método
del Pórtico Equivalente, el sistema de losas se divide en franjas de diseño que
consisten en una franja de columna y la mitad de una o dos franjas intermedias,
como se ilustra en la figura 1.7.
Definición de las Franjas de Diseño
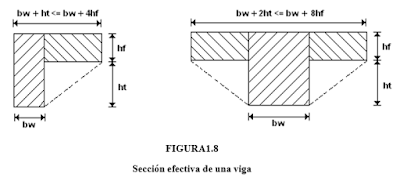
Sección efectiva de una viga
Para los
sistemas de losas con vigas entre sus apoyos, las vigas deben incluir partes de
la losa a modo de alas, como se ilustra en la Figura 1.8. Las constantes de
diseño y los parámetros de rigidez utilizados con el Método de Diseño Directo y
el Método del Pórtico Equivalente se basan en las secciones de viga efectivas
ilustradas.
Espesor Mínimo de la Losa
El Código del ACI propone espesores mínimos de
losa que garantizan que sus deflexiones no sean excesivas. Si los esfuerzos de
corte son elevados, dicho espesor debe ser incrementado. Esta situación se
suele presentar en los sistemas de losas sin vigas. El espesor mínimo de losas
con vigas entre apoyos, es función de αm el cual es igual al promedio de los valores
de αf correspondiente a
las vigas que limitan el paño. El parámetro se determina a través de la
siguiente expresión:
Ln, es la luz libre en la dirección de la luz
mayor entre apoyos para losas sin vigas o entre caras de vigas para losas con
vigas.
El espesor mínimo h para losas con vigas que se
extienden entre los apoyos en todos los lados debe ser:
Para αm
≤ 0.2, se consideran los espesores de la tabla 1.5.
Para 0.2 < αm < 2.0, h no debe ser menor
que:
10.1
Análisis
y diseño de losas perimetralmente apoyadas
10.2.1 Comportamiento
estructural
Las losas
en una dirección se deforman bajo carga siguiendo una superficie cilíndrica
similar a la indicada en la figura 10.5. En este sentido la acción estructural
es principalmente en una dirección, es decir normal a los bordes de apoyo de la
losa. Sin embargo este no es el caso general y muchas veces las losas tienen
dimensiones y están apoyadas de tal forma que se presenta una acción
bidireccional es decir la superficie deformada ya no es cilíndrica sino en
forma de domo esférico y cualquier punto de la losa esta sometido a dos tipos
de curvaturas indicando que existen momentos en las dos direcciones
ortogonales. Para resistir estos momentos la losa se debe reforzar en ambas
direcciones con capas de acero cuyas cuantías aseguren una adecuada capacidad
de carga cuando se someta a las diferentes solicitaciones externas.
Figura 10.5 Accion estructural en una y en dos
direcciones en losas
El tipo mas simple de losa con acción
estructural en las dos direcciones esta representado en la figura 10.2.b. En
este caso la losa indicada se apoya en vigas perimetrales cargueras que van en
los cuatro bordes y se caracterizan porque son muy rígidas y trabajan
monolíticamente con la losa transfiriendo flexión, torsión y cortante. La
rigidez de las vigas de borde garantiza que bajo la acción de las cargas estas
no sufren deformaciones apreciables. Esta hipótesis no se cumple si la losa no
lleva vigas o estas se colocan con
espesor delgado ( se recomienda que la viga perimetral tenga al menos un
espesor igual a tres veces el espesor de la losa).
Si se asumen las consideraciones anteriores se puede visualizar la losa
como un conjunto de franjas imaginarias de ancho “ bx : franjas
paralelas al eje Y ” y “ by :
franjas paralelas al eje X “ que recorren la losa en las dos direcciones y se
interceptan en determinados puntos,
figura 10.6. Al aplicar una carga uniformemente distribuida cualquiera “ q “
sobre la losa es evidente que cierta fracción de esta se transmite en una
dirección mientras que otra parte se transmite en la dirección perpenticular de
acuerdo a las características dimensiónales de la losa. Si se define ahora que
la losa es rectangular con “ la “ siendo la luz corta y “ lb
“ la luz larga y se consideran solo las dos franjas centrales se tiene el
siguiente resultado: “ la deflexión en el punto central de la losa donde se
interceptan las dos franjas imaginarias debe ser la misma por compatibilidad de
deformaciones “. Para demostrar este enunciado se asumirá una losa simplemente
apoyada perimetralmente =>
Figura
10.6 Disposicion de franjas en una losa
en dos direcciones
Las deflexiones de ambas franjas se obtienen de la resistencia de materiales:
∆max .a =
3845.qa..Ela.4I y ∆max .b =
3845.qb..Elb.4I
En la igualdad => ∆max .a = ∆max .b ⇒ qa.la4 = qb.lb4
qa = b44 qb la
|
|
Se demuestra para este caso en particular que
la relación de las cargas en dirección corta y larga es inversamente
proporcional a la relación de las luces elevadas a la cuarta potencia. En otras
palabras la proporción de carga que toma la dirección corta es mucho mayor que
la que toma la dirección larga. Por ejemplo si se tiene una losa con la
= 4.0 m y lb = 5.0 m y se aplica una carga de q = 15 kN / m2 la
proporción es la siguiente:
Es decir la luz corta se lleva aprox. dos veces y media mas carga que la
luz larga o lo que es lo mismo: la luz corta se lleva el 70% de la carga.
En realidad este resultado es aproximado ya que el comportamiento bajo
carga es mucho mas complejo que lo ilustrado, sin embargo nos sirve para
mostrar algunas tendencias en el comportamiento estructural de las losas. La
figura 10.6 muestra también que paralelas a las franjas centrales van franjas
cercanas a los bordes que no solo se deflectan sino que sufren distorsiones a
torsión por el efecto de las vigas de borde. Estas deformaciones por torsión lo
que hace es modificar la capacidad resistente de la losa generando un efecto de
confinamiento lateral que le permite soportar mas carga de la que realmente un
análisis elástico puede determinar. Esta es la razón por la cual los momentos
medidos en losas bajo carga son muy pequeños comparados con los que se obtienen
de un análisis estructural elástico considerando franjas paralelas no
conectadas transversalmente y sometidas a “ qa “ y “ qb
“. Por ejemplo para una losa cuadrada “ la = lb = l “
simplemente apoyada se cumple: “ qa = qb = q / 2. Si solo
se presentara flexión el momento máximo en cada franja seria:
La teoría exacta de la flexión de placas elásticas muestra que realmente
el momento máximo en esta losa es:
Mmax+ = 0.048ql2
Esto significa una disminución en el momento de
aprox. un 25% debido a la presencia de los momentos torsores no considerados en
la ecuación 10.2. Los mayores momentos se presentan cuando la curvatura es mas
pronunciada fenómeno que se inicia en la franja central corta de la losa. Si se
supone ahora que la carga se aumenta hasta sobretensionar la sección mas
critica de esta franja de tal forma que el acero entre en fluencia se produce
inmediatamente su falla, pero si se considera unida lateralmente a las otras
franjas la falla no se manifiesta y por lo tanto se demuestra como de esta
forma la franja esta en capacidad de soportar una carga adicional a la que ella
en forma aislada esta en capacidad de resistir. Esta redistribución de
tensiones generalmente se presenta en el rango inelástico y continuara hasta
lograr que todo el refuerzo bidireccional de la losa entre en fluencia momento
en el cual se presenta la falla. Por estas razones, confirmadas también por
numerosos ensayos, se demuestra que en el diseño de las losas no se requiere
utilizar el máximo momento elástico de diseño de la ecuación 10.3 en cada una de las dos direcciones sino un
valor promedio menor que en muchos casos se acerca a un 75% del valor dado por
la teoría elástica:
M max+ = 0.036ql2
Los mayores
momentos en las losas en dos direcciones se presentan en la mitad de ambas
franjas mientras que la variación de los momentos en cada franja se da en
sentido perpenticular a su dirección como lo indica la figura 10.7. El diagrama
de momentos en cada una de las dos direcciones es valido únicamente en las
franjas centrales porque en las extremas el momento disminuye como se indica en
la figura 10.7. Estas variaciones en el momento máximo se deben realizar en
forma mas o menos realista para que reflejen mas certeramente el comportamiento
bajo carga de estas estructuras. Los momentos en las franjas centrales deben
ser mayores que los de las franjas extremas es decir de las franjas cercanas a
los bordes de la losa.
Franjas Franjas extr. larga extr. larga
Figura 10.7 Definición de franjas y momentos en losas en
dos direcciones
Un análisis mas riguroso de la ecuación 10.1
indica que solo aquellas losas con relación luz larga a luz corta “ lb / la “
menor que 2.0 requieren diseñarse como losas en dos direcciones ya que para
relaciones mayores o iguales a 2.0 la contribución de la luz larga es de solo 1
/ 16 parte de la dirección corta por lo que su comportamiento es prácticamente
en una dirección ( corta). En consecuencia aquellas losas perimetralmente
apoyadas con relación “ lb / la < 2.0 “ o también “
0.5 ≤ la / lb < 1.0 “ son las únicas que deben ser
tratadas como losas en dos direcciones. En este caso se puede considerar como
primera aproximación de diseño que el espesor de la losa sea mayor o igual al
0.55% del perímetro del panel respetivo:
hs ≥ ( perímetro panel ) / 180
10.2.2 Análisis estructural por
el método de los coeficientes del ACI
Si se
utilizan los principios anteriores para determinar por teoría de elasticidad
los momentos en losas bidireccionales es evidente la inmensa cantidad de
cálculos que se deben realizar para cada una de las condiciones de carga y
apoyos en un determinado proyecto estructural. Aun con la ayuda de computadores
esto realmente no es practico ni se mejoran los resultados de los diseños
obtenidos. Es por esta razón que la ingeniería ha adoptado métodos mas
simplificados para determinar las reacciones y los esfuerzos en este tipo de
losas. Según el código ACI-318 todos los sistemas de losa en dos direcciones
ilustrados en las figuras 10.2 y 10.3 pueden ser diseñados por procedimientos
mas elaborados como el método directo o el del pórtico equivalente; sin embargo
se reconoce que en aquellos casos donde se cumplen las particularidades e
hipótesis requeridas se pueden aplicar algoritmos mas sencillos que, reduciendo
notablemente la cantidad de operaciones de calculo, entregan resultados
satisfactorios.
El “ método de los coeficientes del ACI “ fue
originalmente propuesto por Henry Marcus en 1929 y ampliamente difundido en
Europa. En América fue presentado por Paul Rogers en 1944. Este ha sido usado
por los ingenieros calculistas Americanos en forma amplia desde su presentación
oficial en el código ACI 318-63 cuando se requieren diseñar o revisar losas en
dos direcciones apoyadas rígidamente en sus bordes por vigas o muros que
suministren una gran rigidez perimetral. A pesar de que en ediciones
posteriores el ACI no hizo referencia directa a este método ( solo menciona el
método directo y el del pórtico equivalente) si recomienda en general que “ Una losa de puede diseñarse por cualquier
procedimiento que satisfaga las ecuaciones de equilibrio y compatibilidad si se
demuestra que la resistencia de diseño en cada sección de la estructura es al
menos igual a la resistencia requerida por las cargas y se satisfacen los
requisitos de servicio y funcionabilidad exigidos “.
El método utiliza las tablas de coeficientes
10.1, 10.2, 10.3 y 10.4 en donde se presenta la variedad mas practica de cargas
y condiciones de borde. Los valores de las tablas se basan en los cálculos
elásticos anteriormente indicados y tienen en cuenta la reducción de los
momentos por efecto de la redistribución inelástica de tensiones. En
consecuencia el momento de diseño para cada dirección es menor que el máximo
obtenido por elasticidad para esa misma dirección. Los momentos en las dos
direcciones se determinan con la expresión 10.5 en donde “ Ma y Mb
“ son los momentos en dirección corta y larga respectivamente, “ Ca
y Cb “ son los coeficientes de momento para la dirección corta y
larga, “ q “ la carga uniformemente distribuida en la losa, “ la y lb
“ son las luces en dirección corta y larga.
Ma = Ca.q.la2 Mb = Cb.q.lb2
|
El método recomienda que cada recuadro de losa
( otro termino muy utilizado para definir una región interna de losa bordeada
por vigas perimetrales es “ panel “ ) sea dividido en tres zonas para cada una
de las dos direcciones de diseño, una central o media la cual tiene un ancho
igual a la mitad de la luz y dos zonas de borde o de columnas con anchos cada
una iguales a la cuarta parte de la luz respectiva.
DISEÑO DE LOSAS
Pasos del Diseño de Losa en Dos Direcciones:
1.Escoger el tipo de losa a usar
2.Determinar el espesor de la losa
3.Determinar el método de calculo de momentos
4.Calcular la distribución de momentos a largo del ancho
de la losa.
5.Si hay vigas, asignar una porción de momento de la
columna a la viga.
6.Designar el refuerzo para los M de los pasos 4 y 5.
7.Revisar esfuerzo por cortante alrededor de las columnas
Figura 10.11 Reacciones y cortantes en losas en dos
direcciones




















No hay comentarios:
Publicar un comentario